机器学习6——回归与聚类

机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。

---

访问作者github： https://github.com/NefelibataBIGR/Machine_Learning_Notes ，获取笔记代码

• 深度学习 ⊆ 机器学习 ⊆ 人工智能
  • 机器学习是人工智能的一个实现途径
  • 深度学习是由机器学习发展而来
• 应用领域：传统预测、图像识别、自然语言处理
• 理论书：《机器学习》“西瓜书”、《统计学习方法》
• 库：sklearn
• ==模型选择==：
  
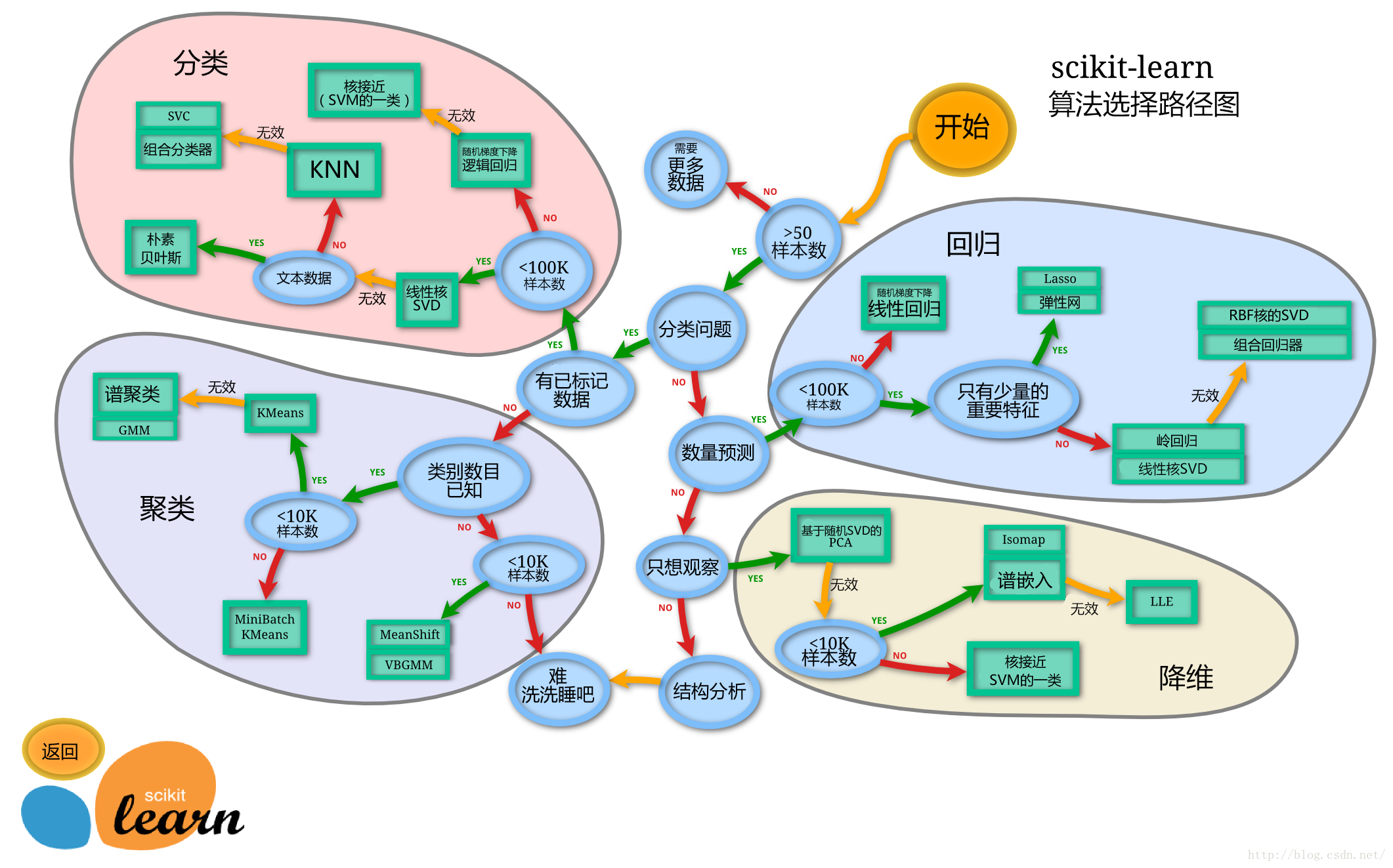
  现在应用广泛的是集成学习算法（多个弱学习器组成强学习器）：
• Bagging（投票制，并行）：随机森林
• Boosting（残差拟合，串行）：GBDT、XGBoosting、LightGBM、CatBoosting

六、回归与聚类算法

具体代码见Python>MachineLearning文件中的==regression_clustering.py==文件

• 回归问题：标签值为连续型数据
• 其他回归算法：Lasso、决策树、部分集成学习算法（随机森林、梯度提升、XGBoost）

1、线性回归

• 用回归方程进行对一个或多个特征（自变量）与标签值（因变量）之间的关系进行建模
  • 一个特征：单变量回归
  • 多个特征：多元回归（一般）

（1）线性模型

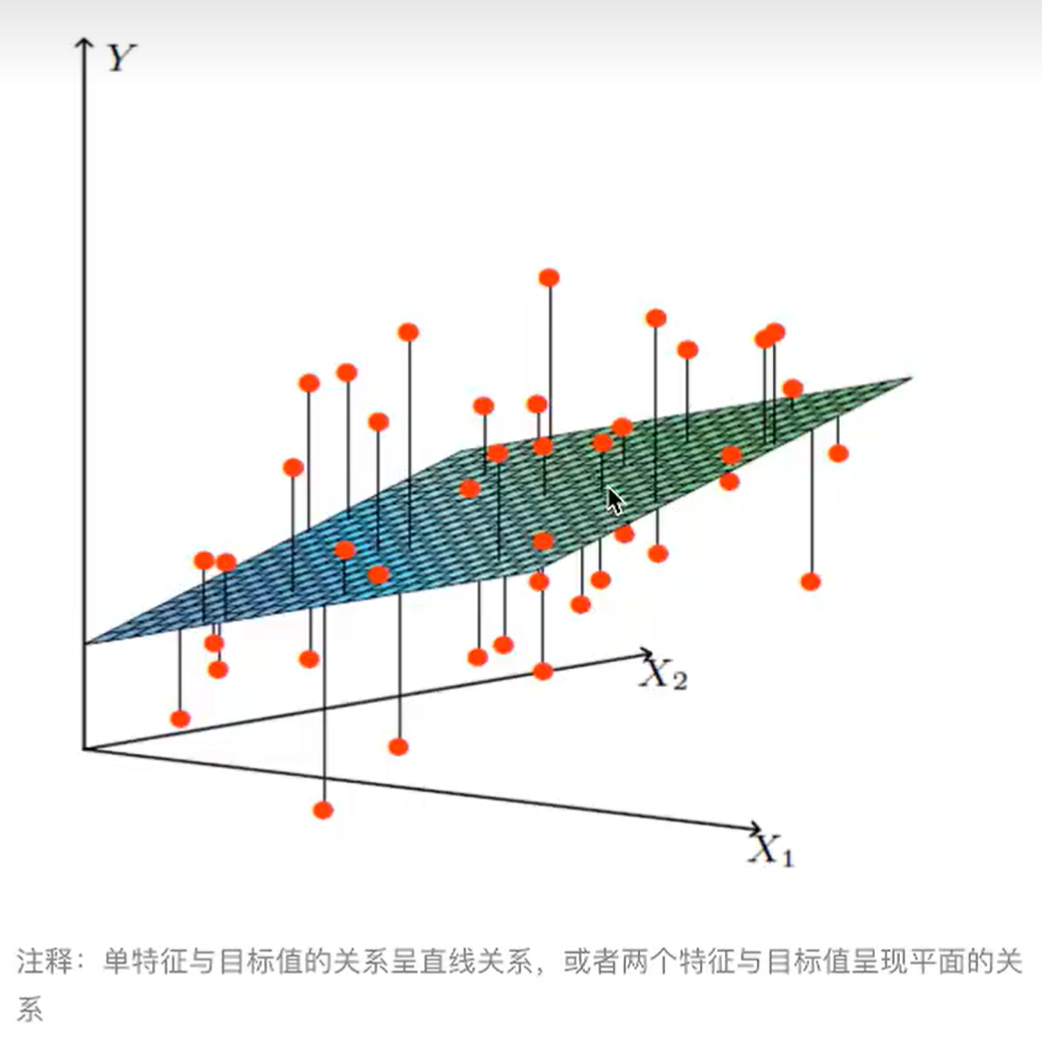
↑两个特征的多元回归示意图

• 广义线性模型：
  • 线性关系：直线、平面等（自变量一次）
  • 非线性关系：曲线等（参数一次）

（2）损失函数

• 目标：求模型参数使得预测准确
• 衡量真实值和预测值之间的误差
• 平方损失函数：
  
• 其他损失函数见：【机器学习】损失函数(Loss Function)全总结(2023最新整理)关键词：Logistic、Hinge、Exponential、Modified Huber、Softmax、L1、L2正则化_huber损失函数-CSDN博客

（3）优化方法

• 正规方程、随机梯度下降（SGD，重要！！！）

①正规方程

• 直接求解W权重：
  

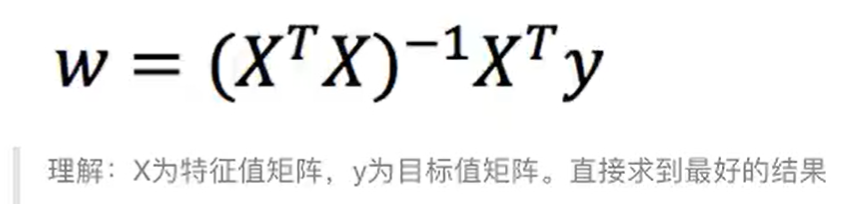
• 理解：损失函数L对每一个特征偏导=0，求得最小值时，W的取值

• 缺点：当特征过多过复杂时，求解速度太慢且得不到结果，时间复杂度高O(n3)

API：

• sklearn.linear_model.LinearRegression(参数)
  • 参数：
    • fit_intercept=：是否添加偏置，一般True
  • 使用：
    • LinearRegression.coef_：查看回归系数
    • LinearRegression.intercept_：查看偏置

②==随机梯度下降==

• stochastic gradient descent（SGD）

• 逐步迭代改进W：（第二个式子后一项应该为对w0求偏导，不是w1）
  

• 缺点

  • 损失函数L只降到局部最小值，而不是全局最小值
  • 很多超参数，需要调参
  • 对特征标准化敏感

API：

• sklearn.linear_model.SGDRegressor(参数)

  • 参数：

    • fit_intercept=：是否添加偏置，一般True
    • loss=：损失函数类型，默认’squared_loss’（平方损失函数）
    • learning_rate=：学习率（eta）填充
      • ‘invscaling’：默认，学习率eta=eta0 / pow(t , pow_t)
        • pow_t：默认=0.25
      • ‘constant’：学习率为常数，eta=eta0
      • ‘optimal’：eta=1.0 / (alpha×(t + t0))
    • alpha=：用来作为’optimal’中的alpha，默认=0.0001
    • eta0=：用来作为’constant’中的eta0，默认=0.01
    • power_t=：用来作为’invscaling’中的pow_t，默认=0.25
    • max_iter=：迭代次数
    • ……

  • 使用：

    • SGDRegressor.coef_：查看回归系数
    • SGDRegressor.intercept_：查看偏置

③其他优化方法

• 梯度下降（GD）：最原始的梯度下降，计算量大
• 随机平均梯度下降（SAG）：SGD的改进
• 理解更多优化算法见：如何理解SAG,SVRG,SAGA三种优化算法 - 知乎

（4）回归模型评估

• 均方误差评估：
  

API：

• sklearn.metrics.mean_squared_error(y_true , y_pred)

  • 参数：
    • y_true：真实值
    • y_pred：预测值
  • return：偏差值

• 其他评估方法见：【机器学习】12种回归评价指标-CSDN博客

- 案例：用SGD预测加州房价

house = fetch_california_housing() # 获取数据集（注意需要魔法）
# print("特征数量", house.data.shape)

x_train, x_test, y_train, y_test = train_test_split(house.data, house.target, random_state=11) # 划分数据集
# 需要比较正规方程和随机梯度下降哪个好，所以随机数种子设置相同

# 标准化
trans = StandardScaler()
x_train = trans.fit_transform(x_train)
x_test = trans.transform(x_test)

# 预估器流程
esti = SGDRegressor() # 可以调参优化，调学习率等
esti.fit(x_train, y_train)

# 得出模型
print("linear_SGDR权重系数：\n", esti.coef_)
print("linear_SGDR偏置：\n", esti.intercept_)

# 评估模型
y_pred = esti.predict(x_test)
print("linear_SGDR预测房价：\n", y_pred)
error = mean_squared_error(y_test, y_pred)
print("linear_SGDR均方误差：\n", error)

输出：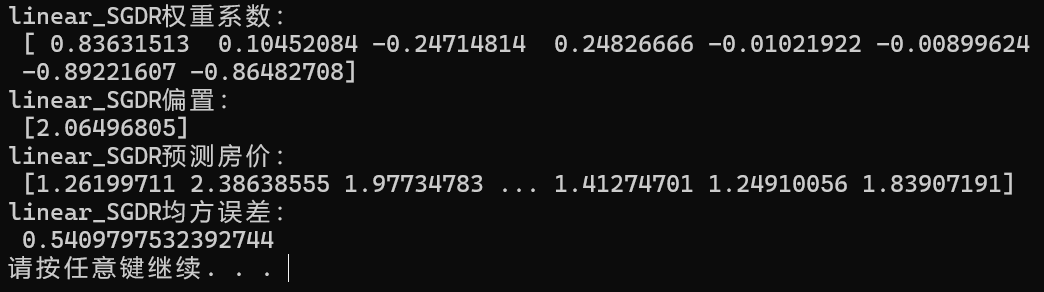

2、欠拟合、过拟合

（1）概念

• 欠拟合：训练集上不能很好拟合，测试集上也不行（模型过于简单）
• 过拟合：训练集上能很好地拟合，但测试集上不行（模型过于复杂）
  
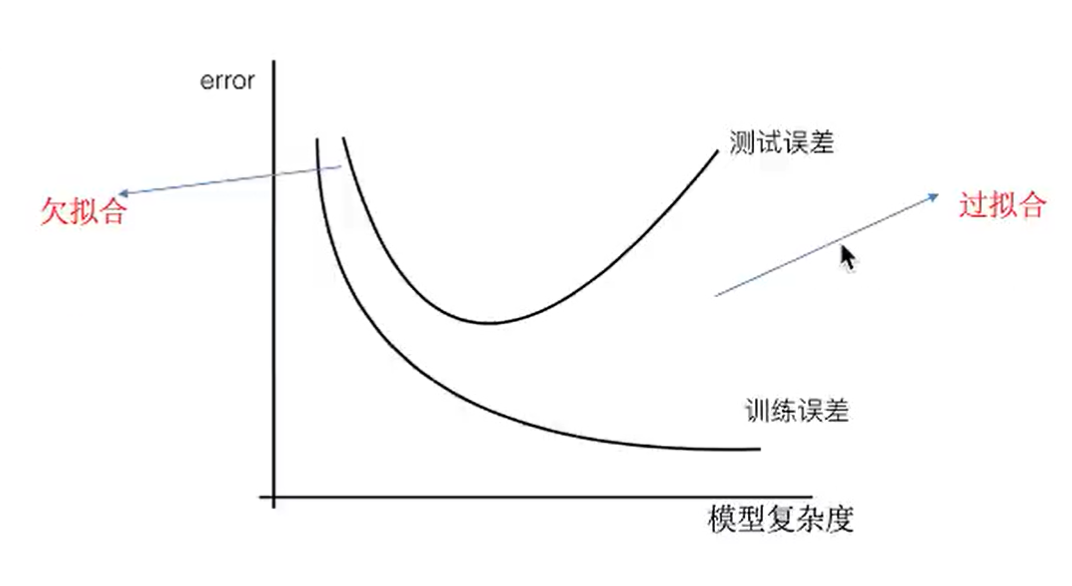
  最好将模型复杂度保持在测试误差最小的时候，也就是↑图中的测试误差最低点

（2）原因及解决方法

• 欠拟合：

  • 原因：学习到的特征过少
  • 解决：增加数据或增加特征

• 过拟合：

  • 原因：学习到的特征过多，有一些嘈杂特征
  • 解决：正则化（针对回归）

• 实际应用中数据量大，主要解决过拟合

（3）正则化

• 解决过拟合问题

• L1正则化：

  • 作用：使某些W直接变为0，删除对应特征的影响
  • 加入L2正则化项之后的新损失函数（LASSO回归）：
    
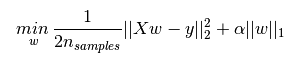
    ↑第一项为原线性回归损失函数，第二项为L1正则化项
    其中L1正则化项为惩罚项，α为正则化系数（惩罚系数）

• L2正则化：

  • 作用：可以使某些W很小，削弱对应特征的影响
  • 加入L2正则化项之后的新损失函数（Ridge回归，岭回归）：
    
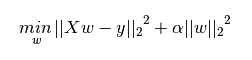
    ↑第一项为原线性回归损失函数（一般会 ÷2n），第二项为L2正则化项
    其中L2正则化项为惩罚项，α为正则化系数（惩罚系数）

• 一般L2正则化最常用

3、岭回归

• 普通线性回归的改进：带L2正则化的线性回归（Ridge回归）
• 能解决过拟合问题

API：

• sklearn.linear_model.Ridge(参数)

  • 参数：

    • alpha=：正则化系数α（正则化力度），默认1.0
    • fit_intercept=：是否添加偏置，一般True
    • solver=：’auto’ 自动选择优化方法（如果数据比较多，自动选择SAG优化器）
    • normalize=：数据是否进行标准化，默认False，True就不用进行特征工程的标准化
    • max_iter=：迭代次数

  • 使用：

    • Ridge.coef_：查看回归系数
    • Ridge.intercept_：查看偏置

Ridge( )相当于SGDRegressor(penalty=’l2’ , loss=’squared_loss’)，只是SGD是随机梯度下降优化方法，Ridge是SAG优化方法，推荐用Ridge

4、逻辑回归、二分类问题

• 属于分类算法

（1）逻辑回归

• Logistic Regression，与回归有关的一种分类算法，应用广泛

• 能很好地解决二分类问题

• 线性回归的输出 -> 逻辑回归的输入，将线性回归的输出（Wx+b）作为激活函数的x输入

• Sigmoid激活函数：
  
  
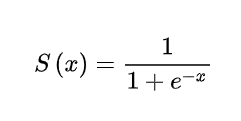
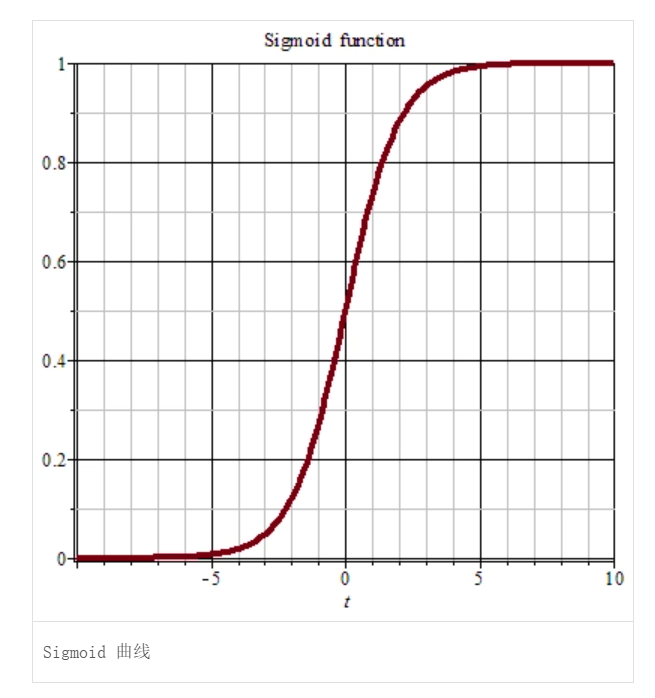
  将 Wx+b 映射到 0-1 区间

• 分类标准：

  • 经过Sigmoid函数映射后>设定的阈值（默认0.5）的认为属于这一类别，<阈值的认为不属于

• 损失函数：

  • 对数似然损失函数：
    
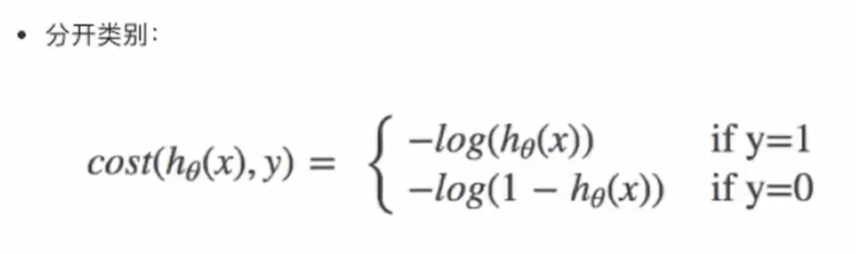
    if y=1表示真实值属于这一类别，hθ(x)表示Sigmoid函数的输出值，log以e为底

  • 也就是（一般会 ÷n）：
    
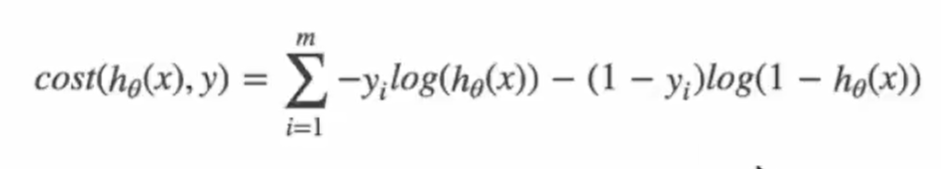
    这个损失函数能够满足逻辑回归的损失函数性质

• 还是用梯度下降法来优化损失函数

API：

• sklearn.linear_model.LogisticRegression(参数)
  • 参数：
    • solver=：优化求解方法
      • ‘liblinear’：默认，自动选择
      • ‘sag’：SAG优化方法
    • penalty=：正则化种类，默认’l2’
    • C=：正则化参数，默认=1.0

SGDClassifier(loss=’log’ , average=True)类似，但是实现的是ASGD优化方法

（2）二分类模型评估方法

• 理想中：用之前分类算法中的准确率（查准率）评估
• 实际：还需要结合查全率（召回率）、AUC等指标
• 样本均衡：精确率、召回率、F1-score
• 样本不均衡：ROC曲线、AUC指标

①精确率、召回率

• 混淆矩阵：
  
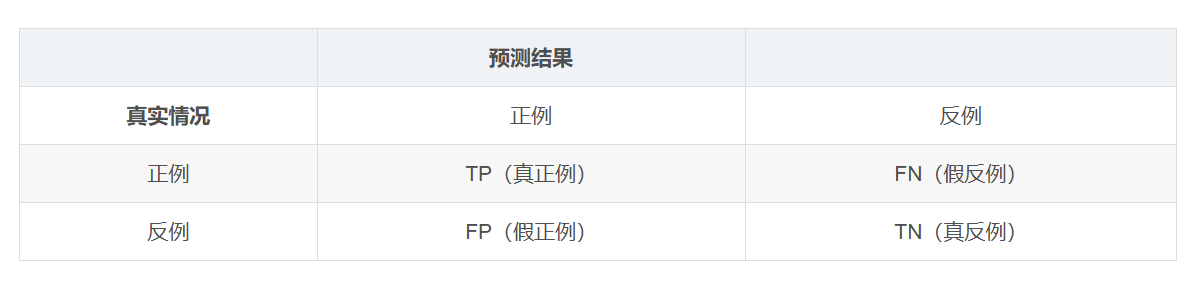
  其中TP+FN+FP+TN=样例总数，TP即True Positive，FN即False Negative

• 精确率P（查准率）：预测结果为正例中实际正例的占比
  
  精确率 P=TP / (TP + FP)

• 召回率R（查全率）：真实情况为正例中预测正例的占比（查的全不全）
  
  召回率 R=TP / (TP + FN)

②F1度量指标

• F1-score，反映模型的稳健性：
  
  综合了精确率与召回率

- API

• sklearn.metrics.classification_report(y_true , y_pred , labels=[ ] , target_names= )
  • 参数：
    • y_true：真实标签值
    • y_pred：预测标签值
    • labels=：分类的类别对应的数字
    • target_names=：数字对应的类别名称（字符串）
  • 比如：
    • report = classification_report(y_test, y_pred, labels=[2, 4], target_names=[‘良性肿瘤’, ‘恶性肿瘤’])
  • return：精确率、召回率、F1-score等指标
    输出样例：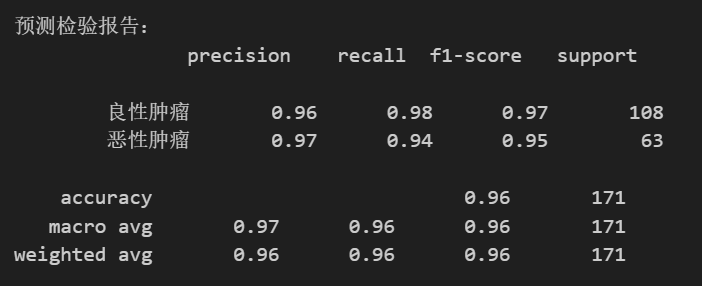
    
    重点关注召回率（recall）

③ROC曲线、AUC指标

• 样本不均衡情况下，精确率、召回率、F1-score不能很好评估模型

• 真阳性率（TPR）：真实情况为正例中预测正例的占比，TP / (TP + FN)，=召回率

• 假阳性率（FPR）：真实情况为反例中预测正例的占比，FP / (TN + FP)
  

• ROC曲线：

  • 横坐标FPR，纵坐标TPR
  • 曲线越靠近左上角（TPR->1，FPR->0），模型越好
    
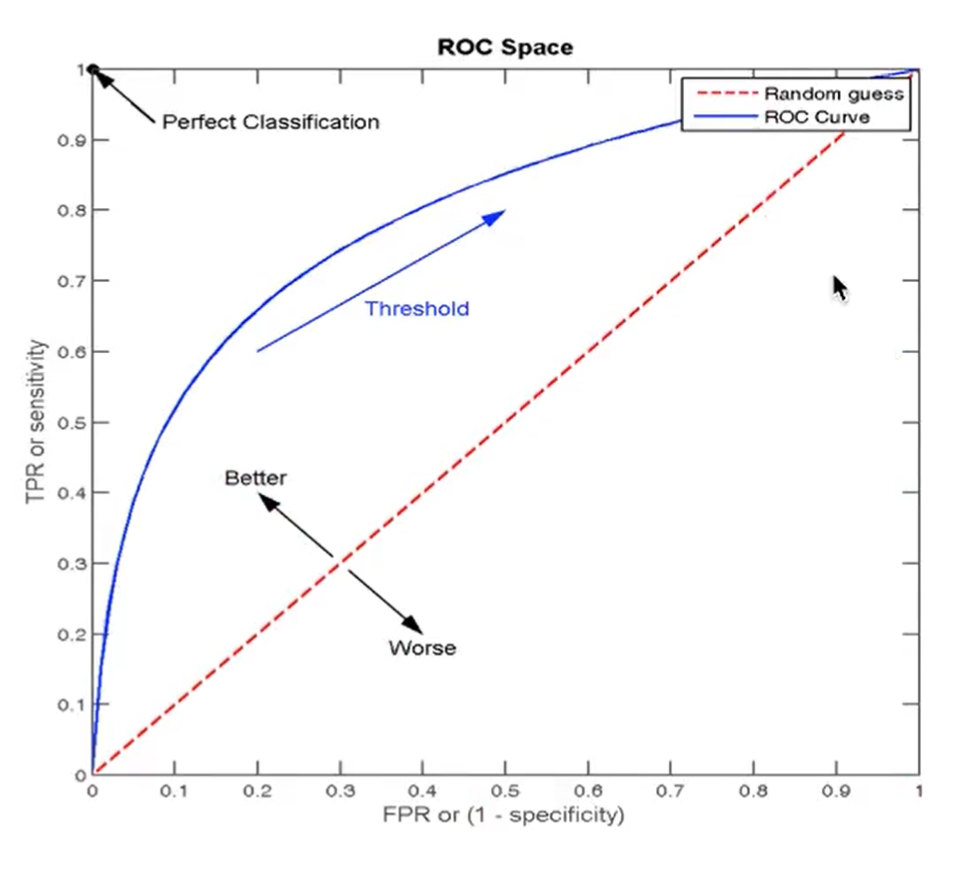
    ROC曲线为蓝色的那条，AUC指标为ROC曲线下方到（1，0）点围成的面积
    红色虚线为随机预测模型（瞎猜），此时AUC指标=0.5

• AUC指标：

  • 概率意义：若随机抽取一个阳性样本和一个阴性样本，分类器正确判断阳性样本的值高于阴性样本的概率=AUC
  • 最小值为0.5，最大值为1（越大越好），若<0.5就反着看（反向预测）
  • 几何意义：ROC曲线下方到（1，0）点围成的面积
  • 非常适合评估样本不均衡时的模型

- API

• sklearn.metrics.roc_auc_score(y_true , y_score)
  • 参数：
    • y_true：每个样本的标签值，必须为0（反例）、1（正例）
    • y_score：预测得分，也可以是正类的估计概率、置信值、分类器方法返回值 (y_pred)
  • return：AUC指标（0~1）

5、无监督学习——K-means算法

• 无监督学习：无标签值
• 包含算法：
  • 聚类
    • K-means聚类
  • 降维
    • PCA

（1）K-means

• 优点：采用迭代式算法，直观、实用

• 缺点：容易收敛到局部最优解

  • 解决：多次聚类

• 应用场景：没有标签值的时候，一般先聚类，便于以后分类

• 步骤：

  1. 随机设置K个点作为初始聚类中心（K值为超参数，表示K个类，看需求，或者调参）
  2. 计算其他每个点到这K个点的距离，将自身标记为属于最近的一类
  3. 标记完所有点后，对K个类的每个类求中心点（求平均值means），作为新的聚类中心
  4. 如果新聚类中心与旧聚类中心相同（如果是第一次就与初始聚类中心比较），就结束，否则重复步骤2、3、4
     
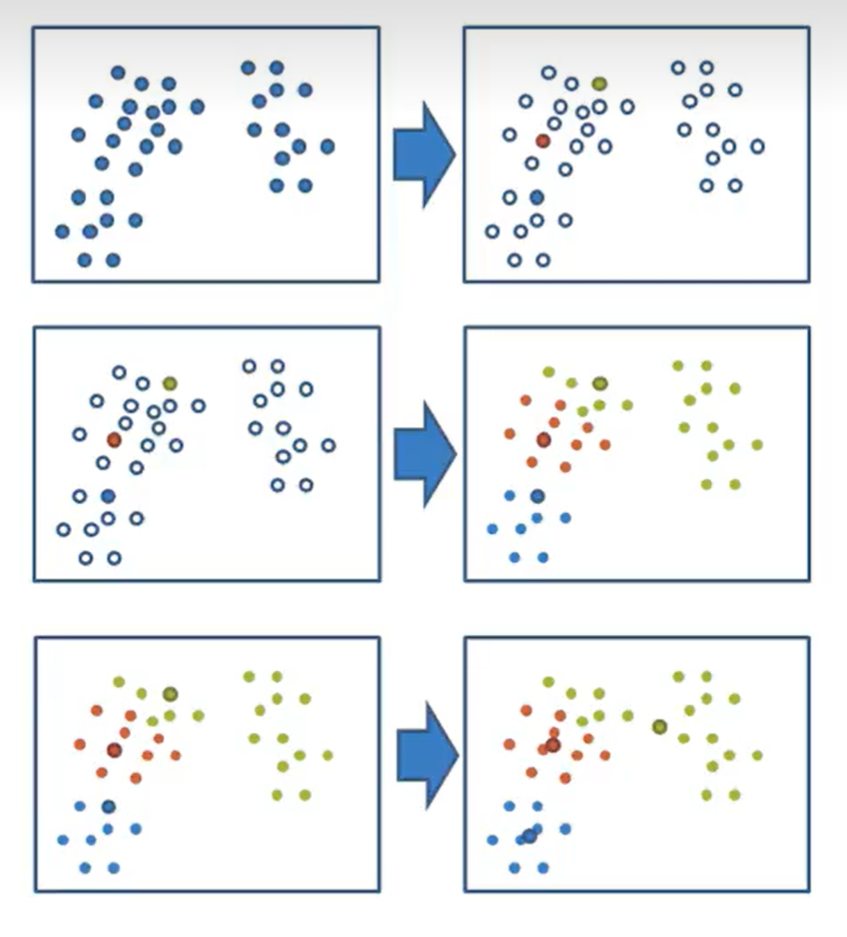
     API：

• sklearn.cluster.KMeans(参数)

  • 参数：
    • n_clusters=：K值，分几类
    • init=：初始化方法，默认’k-means++’
    • labels_=：默认标识的类型，可以和真实值比较（不是值比较）
  • 训练：KMeans.fit(data)：data为特征值，没有标签值，不用传

（2）聚类模型评估

• 轮廓系数：
  
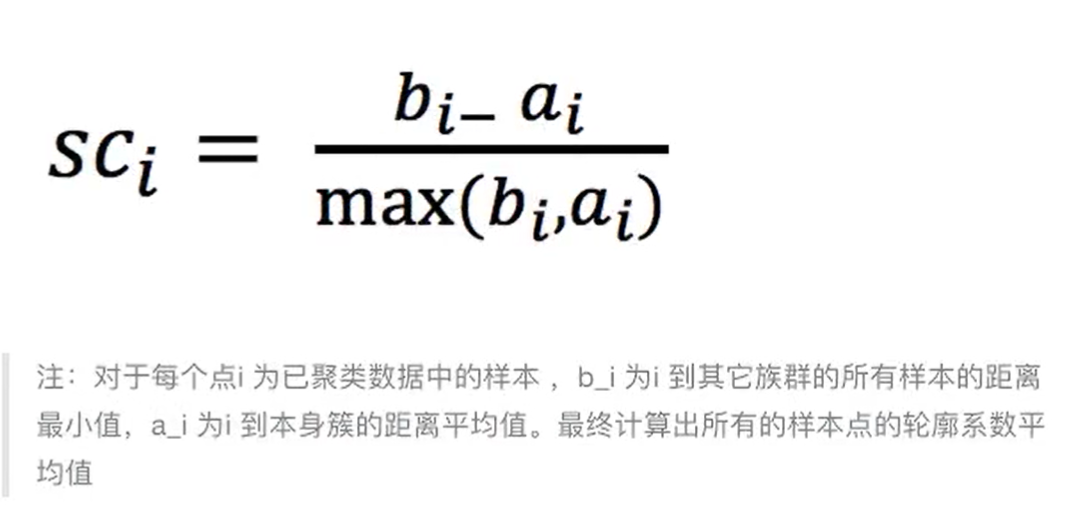
  轮廓系数是对某一个样本而言，bi为这个样本到其他类别样本的距离最小值，ai为这个样本到本类别其他所有样本的距离平均值
  当bi>>ai，SCi=1；bi<<ai，SCi=-1；轮廓系数取值范围[-1 , 1]，SCi越接近 1 模型越好

• 几何理解：
  
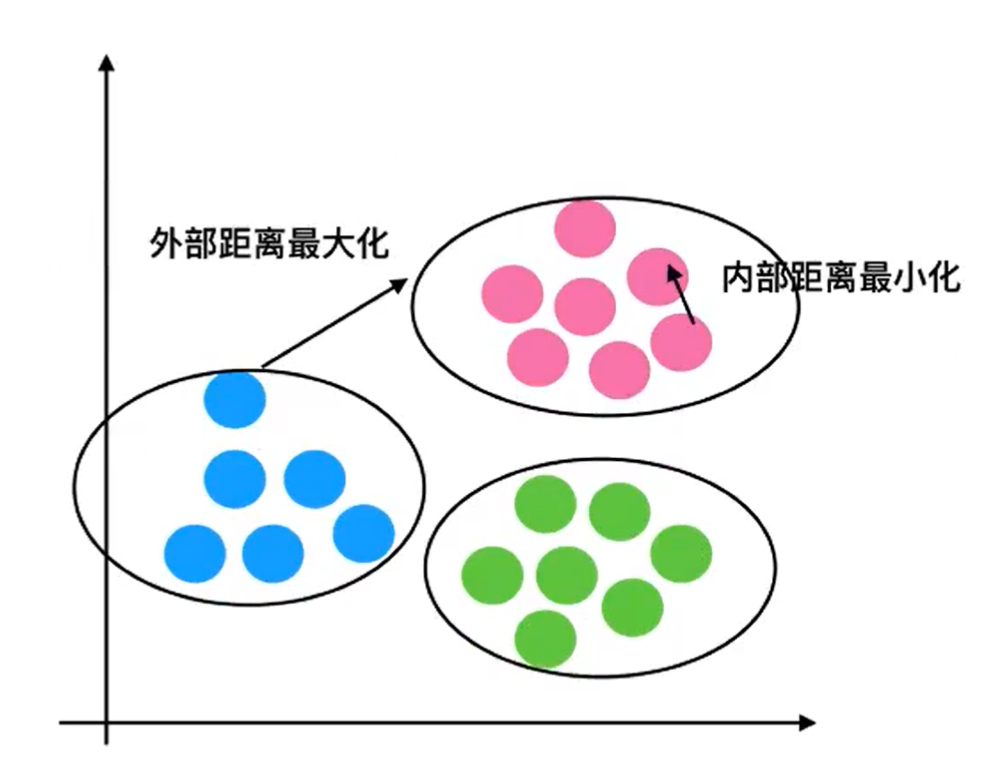
  不同类之间离得远，类内样本间离得近

API：

• sklearn.metrics.silhouette_score(X , labels=[ ])
  • 参数：
    • X：特征值
    • labels：经过聚类标记的标签值，也就是用KMeans.predict(X)得到的y_pred
  • return：所有样本的平均轮廓系数

- 案例：Instacart市场篮子分析（聚类部分）

具体代码见Python>MachineLearning文件中的==instacart.ipynb==文件